This issue of Science & Global Security has two articles focused on uranium, arguably the material that is central to the nuclear age both for nuclear weapons and nuclear power purposes. The International Atomic Energy Agency considers uranium enriched above 20% in the isotope uranium-235 (highly enriched uranium or HEU), to be direct use weapon material for safeguards purposes.
Natural uranium (which contains 0.7% uranium-235) is used as nuclear reactor fuel, especially in plutonium production reactors, and when enriched to various levels in the isotope uranium-235 is used to make fuel for light water power reactors, research reactors and naval propulsion reactors, and for weapons. The first uranium fueled reactors and various uranium enrichment technologies were developed in the U.S. Manhattan Project, and soon afterwards came the first naval reactor. The USS Nautilus, the first nuclear powered submarine, was fueled with 20% enriched fuel when it was launched in 1953, and in 1957 the fuel enrichment was increased to 40%. Today, the United States and Britain use fuel enriched to over 90% for naval reactors, while Russia and India use mostly less enriched HEU. France and China use fuel with less than 20% enrichment (low enriched uranium, LEU), while Brazil is developing a naval reactor program.
The first article in the issue is "Impact of Fuel Enrichment on Key Naval Reactor Characteristics and Nonproliferation Concerns" by Ernesto Mané. It uses neutronics modeling to assess reactor core life, reactivity margins and plutonium inventory for three models of a generic compact three-zoned 50MWt pressurized water reactor core with mean uranium enrichments of 7.4%, 14.8% and 29.6% respectively and burnable neutron poisons. The article shows that low enriched uranium naval reactors could sustain criticality for 5-7 years at full-power and operating at a more realistic 20% capacity factor some cores could run for over 35 years, meaning that no refueling would be required over the operating life of the vessel. The modeling also show that the LEU reactors can overcome xenon poison transients and so allow naval reactors to produce power quickly for military operations requiring sudden acceleration. The results strengthen the case that it is feasible for future military naval reactors to be designed solely for LEU fuel and that countries that rely currently on HEU for naval propulsion could move to LEU fuel. A new constraint that is identified is the larger end-of life plutonium inventory in an LEU core that would need to be considered for safeguarding such spent naval fuel. There are, however, currently no safeguards on military naval spent fuel.
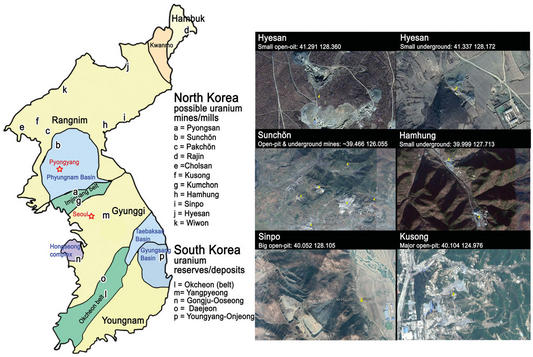
The second article in the issue deals with improving the estimates for uranium mining and milling in the Democratic People's Republic of Korea (DPRK) as a way to constrain the scale of its possible fissile material production for nuclear weapon purposes. Access to sufficient quantities of natural uranium was a key challenge in the early period of nuclear weapon development. Uranium was considered to be so scarce and so important that in June 1944 President Roosevelt of the United States and Prime Minister Churchill of the United Kingdom established the Combined Development Trust as an international effort "to control to the fullest extent practicable the supplies of uranium and thorium ore" and so deny it to other states. Large scale prospecting eventually showed uranium to be far more abundant at lower costs than initially expected.
In "Geologic Analysis of the Democratic People's Republic of Korea's Uranium Resources and Mines," (Free PDF Sulgiye Park, Allison Puccioni, Cameron L. Tracy, Elliot Serbin and Rodney C. Ewing use a detailed review of the geology of DPRK based on a variety of geologic maps, including the Geological Map of Korea produced by the DPRK Geological Institute Academy of Sciences in 1993, to estimate the DPRK's potential uranium resources. The analysis predicts the uranium deposit type and average ore grades at the two mines declared by DPRK in 1992 and at several alleged uranium mines - the estimates for the average ore grade range from about 0.001-0.04 weight % uranium, with an upper bound of 0.2 weight % uranium, significantly lower than much previous analysis. Translating the potential geological availability of uranium into an assessment of ore volume and production remains a challenge, however, and the authors highlight the limits and possibility of satellite imagery to improve estimates of mining and uranium milling operations.
